Leonardo of Pisa, known more commonly as Fibonacci, was a monumental figure in the annals of mathematics. Born around 1170 in Pisa, Italy, Fibonacci’s work transcended the realms of arithmetic, introducing Europe to a novel numerical system and unveiling a sequence that found echoes in nature and art. This article aims to traverse the illustrious life and contributions of Fibonacci, whose legacy continues to resonate through the corridors of mathematics and beyond.
Born into a merchant family, young Fibonacci had the privilege of traveling across the Mediterranean. His father’s trade activities enabled him to study under the leading Arab mathematicians of the time. This exposure fostered a deep love for numbers and a recognition of the limitations of the Roman numeral system prevalent in Europe.
In 1202, Fibonacci published “Liber Abaci” (The Book of Calculation), which was a groundbreaking work. Through this book, he introduced the Hindu-Arabic numeral system to Europe, which included the revolutionary concept of zero and a positional notation system. “Liber Abaci” showcased the superiority of this system over the Roman numerals, particularly in commercial bookkeeping, calculation of interest, conversion of measurements, and other computations necessary for the burgeoning trade economy of the time. In “Liber Abaci,” Fibonacci also introduced what would later be termed the Fibonacci sequence while examining a hypothetical problem concerning rabbit breeding. This sequence, where each number is the sum of the preceding two (0, 1, 1, 2, 3, 5, 8, 13, …), unveiled a mathematical beauty that found reflections in the natural and artistic world, from the arrangement of leaves and flowers to the proportions in classical architecture and art.
Fibonacci’s genius was recognized by his contemporaries, including the Emperor Frederick II, who enjoyed engaging with intellectuals of the time. His work in arithmetic and algebra were groundbreaking, paving the way for future mathematicians and scientists. The legacy of Fibonacci endures, with modern-day applications of his sequence found in diverse fields like computer science, financial markets, and even in the aesthetic realms of music and art.
Connection between the Golden Ratio and Fibonacci
The Golden Ratio, often denoted by the Greek letter phi (φ), is a mathematical constant that has captivated mathematicians, artists, architects, and naturalists for centuries. Represented numerically as approximately 1.618, the Golden Ratio is often associated with aesthetic beauty and natural harmony. The origins of the Golden Ratio can be traced back to ancient civilizations. The Greeks, particularly, were known to have a profound appreciation for geometric beauty. The mathematician Euclid, around 300 BCE, provided the first known written definition of the Golden Ratio in his seminal work “Elements”. However, evidence of the Golden Ratio exists in architectural and artistic works of earlier civilizations, indicating a prehistoric awareness of this divine proportion. The Golden Ratio is derived from a simple geometric relationship. If a line is divided into two parts, a and b, such that the whole line divided by the longer part (a) is equal to the longer part (a) divided by the shorter part (b), the common value is φ (phi), which is approximately 1.618. Mathematically, it is expressed as (a+b)/a = a/b = φ.
The intriguing aspect of φ is that it has an infinite decimal representation, 1.618033988749895…, and it is one of the most irrational numbers, making it difficult to express as a simple fraction or a repeating or terminating decimal. The Fibonacci sequence is intimately connected with the Golden Ratio. As one progresses through the Fibonacci sequence, the ratio of successive terms increasingly approximates the Golden Ratio. Specifically, as n approaches infinity, the ratio of the (n+1)th term to the nth term approaches φ.
The Fibonacci sequence: a technical analysis tool in Trading
The Fibonacci sequence has found its application far beyond the realms of mathematics. In the world of trading and stock market analysis, the Fibonacci numbers play a critical role, especially in technical analysis where traders seek to predict future price movements based on historical data.
The application of Fibonacci numbers in technical analysis is often traced back to the Fibonacci Retracement Technique. This technique utilizes the ratios derived from the Fibonacci sequence to estimate price movements of stocks. The Fibonacci retracement levels are seen as significant support and resistance levels where a market might turn around.
The exact individual who introduced the use of Fibonacci numbers in trading is not clearly identified in the historical records. However, the concept of using Fibonacci numbers and ratios in trading and technical analysis seems to have developed over time as traders realized the potential of these ratios in forecasting market behavior.
The followings are the most used techniques that deploy Fibonacci numbers in technical analysis:
Fibonacci Retracement: This is the most common application where certain ratios from the Fibonacci sequence are used to identify potential support and resistance levels. Traders use these levels to identify entry and exit points.
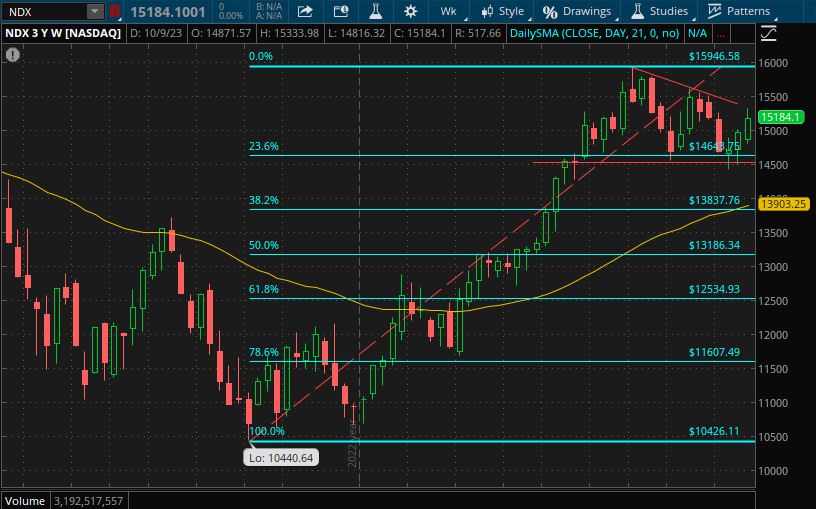
Fibonacci Extensions: These are used to predict the levels of future price movements beyond the current price range.
Fibonacci Arcs and Fans: These tools help traders in identifying potential support and resistance levels based on time and price.
The Chartered Market Technician (CMT) Association, a global credentialing body for technical analysts, includes Fibonacci analysis in its body of knowledge. This recognition underscores the significance and the mainstream acceptance of Fibonacci analysis in modern trading.
Also to consider the relationship between Nelson Elliott’s wave theory and the Fibonacci sequence is a fascinating blend of market technical analysis and mathematical theory. Nelson Elliott, in the early 20th century, propounded the Elliott Wave Theory, which posits that markets move in repetitive cycles, and these cycles are a reflection of investor sentiment and mass psychology. The theory identifies a recurring fractal structure in market price movements, which is divided into impulsive and corrective waves.
Here are some of the connections between Elliott Wave Theory and the Fibonacci sequence:
Wave Structure: Elliott discovered that the wave structures in market prices often consist of a pattern of five waves in the direction of the main trend followed by three corrective waves, a 5-3 move. The Fibonacci sequence is evident here as 5 and 3 are numbers in the Fibonacci sequence.
Wave Relationships: The relationships between the waves, as posited by Elliott, often conform to Fibonacci ratios. For instance, it’s common to find that the length of the waves is related by Fibonacci ratios like 0.618 or 1.618.
Retracement Levels: In Elliott Wave Theory, corrective waves often retrace a portion of the preceding impulse wave, and these retracement levels often correspond to Fibonacci retracement levels such as 38.2%, 50%, or 61.8%.
In modern times, various authors and trading strategy developers have contributed to the popularization and further development of Fibonacci-based trading strategies. For instance, a book by Robert Fischer provides an in-depth examination of blending the Fibonacci series with other trading tools for trading securities. Whether employed by seasoned traders or recognized by professional bodies like the CMT Association, the Fibonacci sequence continues to be an indispensable tool in the world of technical analysis.